A BEGINNER’S GUIDE TO MULTICAST, ON JUNIPER ROUTERS. PART 1: THE THEORY.
Well, the internet has spoken. Millions of people (78 people) took to the polls, and democratically DEMANDED that I write about how to configure multicast on Juniper routers.
I mean, look at that result. Look at it. We’re talking about nothing less than an overwhelming majority of the entire population of the planet.
Now, as I’m sure you know, I have a truly deep hatred for democracy. Why? Well, you’ll be fully aware already that I’m the only real person in the universe, and that you are all mere elements of the computer simulation I’m stuck inside. I am the protagonist of life. You, the person reading this, are at best an actor, and at worst a dream – a terrible, terrible dream. With that in mind, it surely makes sense that only my opinion should count, and the entire world should be set up to precisely match my personal desires and beliefs. Prove me wrong, cowards.
Nevertheless, this one time I will listen to you, the little people, and “give you” what you “want”.
In future posts we’ll be getting hands-on with some sweet Juniper multicast configuration. But first, we need to make sure we’re okay with the theory. Multicast has been written about countless times before, by people far smarter than me. So in this post I’ll just briefly introduce all the concepts, protocols and terminology we’ll need to know, focusing on IPv4 for now, so that you’ll understand enough to follow the configuration that we’ll do in future posts. Whether you’re studying for JNCIP/JNCIE, or if you’re just interested in how multicast works, I’m hoping you’ll get a lot out of this series.
The theory below is divided into sections, so you can easily skip stuff you know, and read just the bits you need to refresh your memory. Not that you need it: as a computer simulation, you do of course have access to the entire sum of all human knowledge and history. But for now, I’ll humour you.
Sound good? “Yes Chris. Yes it does.” Great! Let’s do it.
THIS POST IS LONG – SO TAKE YOUR TIME!
I wanted to make one post that covers all the multicast theory that a beginner will need. I like the idea of having one single post that will get people started, a post folks can share and say “this taught me how multicast works”.
However, the result is that this post is fairly long.
If you’re brand new to multicast, my advice to you: take your time, read it slowly, and have fun learning about it! Don’t worry too much if bits don’t make sense right away. This post introduces a lot of concepts fairly quickly. It’s a lot to take in! Perhaps you might prefer to read half of the post now, and the other half another time. Re-read bits if you fancy. There’s nothing wrong with reading it all in one go, of course – but maybe re-read it again tomorrow. I promise* you’ll be a multicast pro in no time at all. That’s the Network Funtimes Guarantee**!
(*Not a promise.)
(*In no way is this a guarantee.)
A REMINDER: UNICAST AND BROADCAST TRAFFIC
You probably already know what unicast traffic is. Uni, meaning one, refers to the fact that the source of the traffic is sending to only one destination.
For example, when you downloaded this web page, it went from my web hosting company directly to you. When you download cute cat pics, those pics go in one direction: from a server, to you. When you watch the latest episode of Beef Inspectors on Netflix, that video is going from Netflix to you, and only you. You’re the only person in the world that watches Beef Inspectors. It’s your favourite show.
The Netflix example is interesting: lots of people watch individual video streams. Even if two people happen to press play on the same video at the same time, it’s still sent twice, once to each person. Even if both people are coming from the same public IP – for example, if they both sit behind the same NATted connection – even in this situation, two separate streams are sent. The fact that two people are visiting Netflix at exactly the same time is just a coincidence.
As well as unicast, we can also broadcast our traffic. This is when traffic is sent to everyone on a LAN, whether they want it or not. You will rarely need to send broadcast traffic yourself, but your computer frequently does it to discover other hosts on your local network. The payload of each broadcast packet has to be processed by each host to discover whether or not the traffic is interesting to the host. Easy to send; inefficient to receive.
WHAT IS MULTICAST?
Multicast is something in between unicast and broadcast.
For a start, multicast senders generally don’t care if anyone is interested in receiving their traffic: the sender sends it anyway, and sends it once and only once.
Once it’s been sent by the sender, the traffic can then go to no-one, or just one person, or two people, or three people, or four people, or five, or six, or… okay, you get the idea. The point is, any number of people may or may not receive it, all around the network.
To understand this concept, let’s think about live internet TV, where potentially millions of people might all be watching the same channel at the same time via the internet. All those customers could be with one ISP, and many of them could be watching in HD, or even 4K definition.
Imagine if this traffic were sent by unicast. In this case, the one sender sends the same packet MILLIONS of times, to many millions of receivers. Can you imagine the ridiculous amount of resources it would take to send the same HD stream to so many people, sending the same packet individually, millions of times, with the only difference being the destination IP address? What a shameful waste of resource. You’d need an enormous cluster of servers simply to be able to generate so much traffic, and that’s not to mention the routers and the bandwidth required along the way.
In a time of climate change, does the idea sit happy with you to think about how much electric, how much CPU and memory, how many cables and networking devices it would take to get this traffic to everyone?
IF ONLY THERE WAS A BETTER WAY. (Spoiler: there is.)
HOW DOES MULTICAST WORK?
So, multicast is when one source sends to zero, one, two, all the way up to potentially millions of receivers. The difference between unicast and multicast is that regardless of the number of receivers, the sender only sends the traffic once.
When the traffic arrives at the next networking device in the chain – usually a router, but occasionally a switch – the traffic is duplicated, to be sent once and only once down each link to either a directly-connected receiver, or a link that hosts a path to an interested receiver.
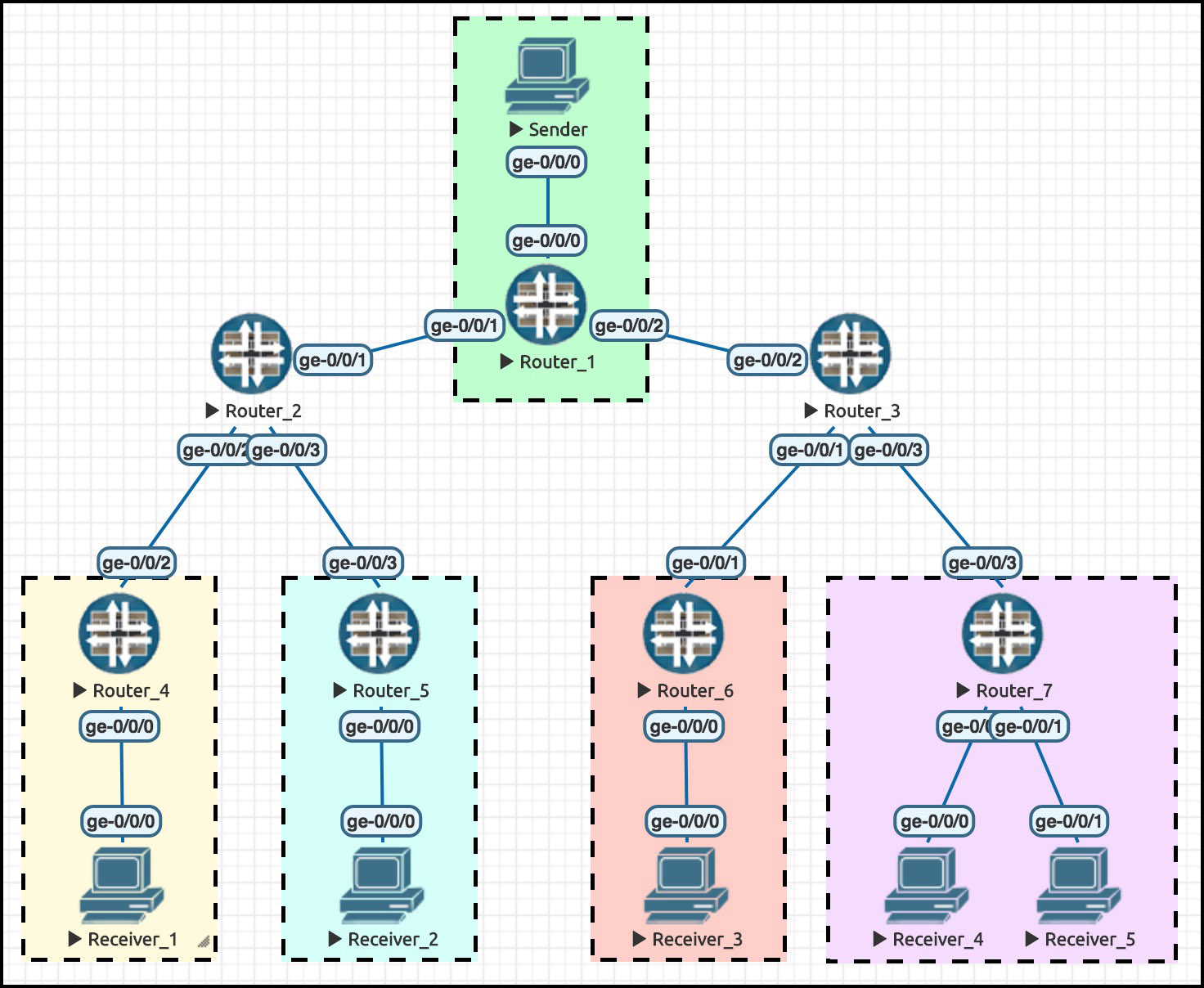
For example, in this diagram we have one sender sending to five receivers. Let’s follow the path the traffic takes from sender to receivers.
The sender sends one single copy of the traffic to its default gateway, Router 1. At this point, Router 1 duplicates the data. The packet is sent once down the link to Router 2, and also once down the link to Router 3. The Sender only sent one packet; Router 1 duplicates it.
Router 2 also duplicates it, sending it once to Router 4 and once to Router 5, who both forward it on to their receivers.
Router 3 also duplicates it, sending it once to Router 6, and once to Router 7. It’s interesting that Router 3 only sends a single copy of the packet to Router 7, even though Router 7 itself has two receivers connected to it. This is fine: Router 7 will duplicate the packet one final time, sending one copy to each of its receivers.
Multicast nerds refer to multicast topologies as a tree, with the sender at the top, sending traffic downstream to the receivers. Each link potentially becomes a branch in the tree, where the traffic can duplicate and spread. Personally I’ve always thought that analogy was a bit weird, because trees are rooted from the bottom, not from the top. This is more like an upside-down tree. Like the kind of trees they have in Australia.
The terms upstream and downstream make more sense when you think about a waterfall, with traffic flowing down from a source.
Now at this point you may be wondering: how on earth did that top router, Router 1, the sender’s default gateway, know to send the traffic to Router 2 and Router 3? To answer that, you need to know about two elements of multicast: the special multicast address range, and the protocols.
THE MULTICAST ADDRESS RANGE
The wizards of the internet dedicated an unnecessarily-large block of IPs specifically for multicast: 224.0.0.0/4. That’s 224.0.0.0 all the way up to 239.255.255.255.
GOOD JOB WE’RE NOT RUNNING OUT OF IPv4 ADDRESSES, OTHERWISE THIS MASSIVE BLOCK OF MAINLY UNUSED IP ADDRESSES WOULD SEEM VERY SILLY INDEED.
At this point I have a favour to ask you: you need to free your mind of something you’ve come to take for granted in networking. You see, these IP addresses aren’t “addresses” in the usual sense, like the kind you can route to, the kind you can assign to an interface. This big block of IPs is also not the kind that can be subnetted into smaller blocks and deployed to a LAN in the way you’re familiar with, blocks assigned to a part of the network with multiple machines in the same shared layer 2 domain. Finally, these addresses cannot be bought and sold and owned by companies.
Rather, each individual /32 address is called a group. They’re not bundled up into bigger subnets like unicast addresses are: instead, each /32 is unique, and beautiful.
Each individual multicast IP represents one single group, and hosts indicate that they’re interested in receiving traffic from a certain group. There’s no advantage to using a block of addresses – aka groups – within a particular subnet, for example using a /24 of IPs from within the multicast range, because each address represents a unique multicast stream, and that stream could be coming from anywhere, and be sent to many receivers in many different locations.
Even if you did happen to have 256 multicast streams, and made each one part of the same /24, they’d still be stored individually in your router’s memory. There might be an advantage just in terms of remembering what addresses you’re using, but my point is that there’s no subnet aggregation for efficiency here.
This is why you’ll often hear people say that unicast routing involves sending traffic TOWARDS a destination, whereas multicast traffic involves sending traffic AWAY FROM a source. There’s no specific destination in mind; the traffic is sent from the source, and is forwarded on to anyone who wants to hear it. That’s why we tend to use the word destination in unicast, and receiver in multicast.
For the most part, there’s nothing interesting about any individual group. For example, there’s no special multicast addresses that indicate your geographical location, or blocks that are owned by one company. However, there are blocks of IPs that have indeed been designated with special purpose. In this early stage of your epic multicast journey it’s not too important to memorise them, but you might be curious about a few key ones.
For example, any address in the 224.0.0.x range never leaves your layer 2 network, and almost all of these addresses are already reserved for special functions. For example, you’ve probably seen addresses like 224.0.0.5 and 224.0.0.6 used in OSPF. The traffic is sent to, and processed by, anyone interested in that group – but even if your router is running a multicast protocol, it will never forward it out of your local network.
Another example is the entire 232.x.x.x range. This entire range is reserved for something called source-specific multicast, which we’ll learn about later on.
There’s LOADS more we could talk about here. We could talk about the way that multicast addresses convert to MAC addresses, or some of the other reserved addresses. And in future posts, we will. But the purpose of this post is to introduce you to just enough theory that we can start getting hands-on with the configuration. So, let’s move on, and talk about the two primary protocols that multicast uses: IGMP, and PIM.
A QUICK INTRODUCTION TO IGMP
Within a LAN, hosts use IGMP, or the Internet Group Management Protocol, to indicate that they want to receive multicast traffic being sent to a particular group. Notice that the M stands for Management, not Message. Don’t confuse it with ICMP!
IGMP is the protocol that hosts use to talk with their default gateway. In future posts when we come to configure IGMP we’ll see that there’s three versions of this protocol, each giving you more control and more options.
Routers on a LAN periodically send out something called a General Membership Query, which basically asks all the hosts to tell the router which multicast groups they’re interested in receiving traffic for.
In IGMPv2 our routers can also send out Group-Specific Membership Queries, which, surprisingly, queries people about whether they’re interested in a specific group!
Meanwhile, our plucky hosts send out Membership Reports. These are messages indicating what groups the host is interested in receiving traffic from.
In addition, our hosts can also send out something called a Leave Group message, which… hmm, actually I can’t remember what that message does. I wish I could work out the purpose of this message from its name. “Leave Group message”. Hmm. What could it possible do?? Hmmmmmm. Oh well, I guess it will have to remain a mystery.
By the way, there’s actually a special name in multicast for the default gateway of an interested receiver: we call it the LHR, or Last-Hop Router. As the name suggests, this router is the last layer-3 hop in the path between sender and receiver. Only a subnet with receivers should live beyond the LHR.
(As you might guess, the default gateway of the sender is called the FHR, or First-Hop Router.)
(As of 2019 there is no name for the most handsome router on the network. However, I’ve been reassured by the IETF that they are working very hard on solving this problem.)
Wow, we introduced a lot of new types of message there! And soon we’re going to introduce a few more. But don’t worry in the slightest about memorising them just yet. That will come later on, as we get hands-on. For now, just be aware that there are various messages sent around the network to indicate that various hosts and routers want to join or leave a tree, and that in addition there’s a few extra messages for special occasions. As long as you know that, you’re golden for now.
A QUICK INTRODUCTION TO PIM
When a router receives an IGMP Membership Report from a host – remember, that’s the message a host sends to indicate that it wants to receive traffic for a particular multicast group – the router then sends this request out to other routers, up the tree. Interestingly though, the request from the router isn’t sent as an IGMP message.
Instead, between routers we have a different protocol: PIM, or Protocol-Independent Multicast. PIM is used to build the tree we talked about earlier. The “Protocol-Independent” bit means that it works regardless of whether you’re running IS-IS, OSPF, or any other internal routing protocol. You could even do it by smoke signals, if your router supports IP Over Smoke Signals, as defined in RFC 69-420.
Some of the messages in PIM are similar to the ones in IGMP. For example, PIM routers send Join Messages to indicate that they’re interested in receiving traffic from a group. They also send Prune Messages to indicate that they want to leave a group. BONUS FACT: technically these are both the same message. PIM Join/Prunes bundle both joins and prunes into one big message. You’ll often hear them talked about as if they were separate messages though, to keep things logical. There’s other message types too, which we’ll get to in future posts.
There’s actually four different flavours of PIM, and three in particular that you’ll want to know about.
PIM Dense Mode does something that’s almost – almost – like broadcast. The source sends the traffic to is default gateway – aka the first-hop router in the path – at which point the FHR sends the traffic downstream to every link of every router on the tree, even if there’s no-one interested in receiving the traffic! It’s up to the individual routers to prune themselves off of the tree if they don’t have any receivers.
Dense mode is very easy to configure, but not necessarily the best in terms of efficient bandwidth.
PIM Sparse Mode is the opposite: once again the source sends the multicast traffic to its own default gateway, but this time the FHR only forwards it on if receivers have actively indicated an interest. If no-one wants it, the packets are dropped by the FHR. And if people do want it, the traffic is forwarded only down the links that directly or indirectly host interested receivers. Sparse mode is used WAY more than dense mode in the real world.
There’s also a hybrid version called PIM Sparse-Dense Mode, which is mostly sparse mode, apart from a few group addresses which are treated as dense mode. There’s a special use case for this, which we’ll learn about another day.
AN INTRODUCTION TO RPF CHECKS
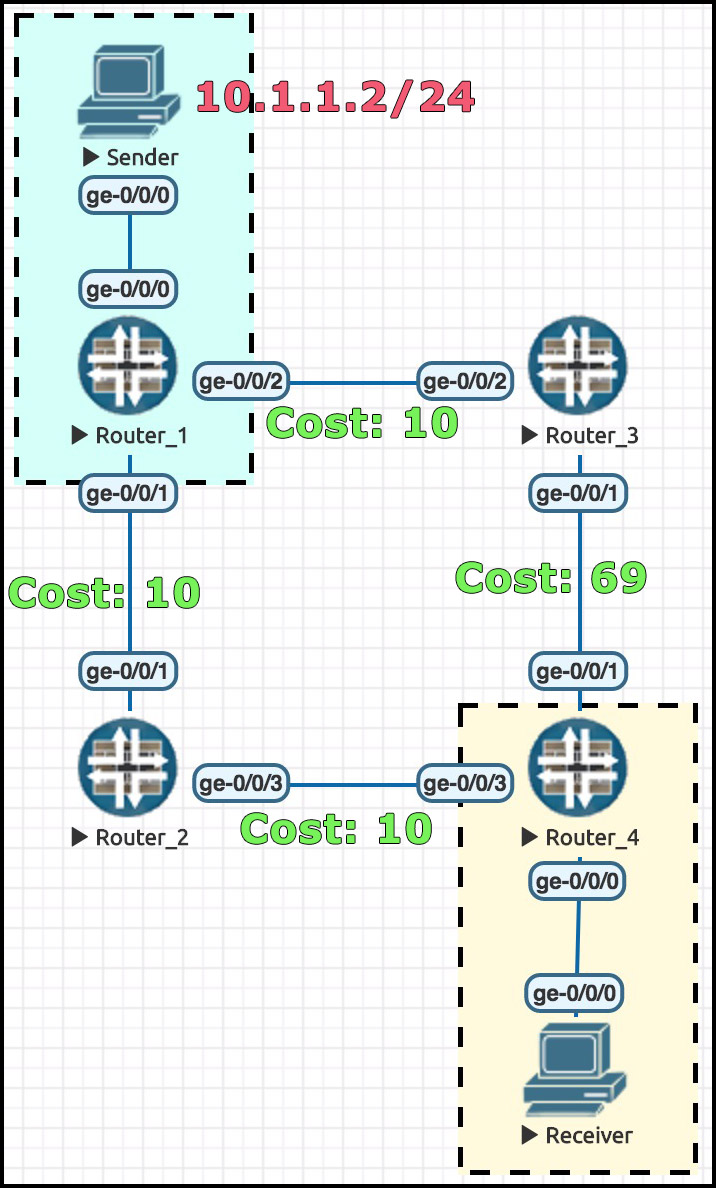 Take a look at this diagram, and imagine that every router is in Dense Mode. Traffic goes from Sender to Router 1, at which point it’s sent out to both Router 2 and Router 3. Both these routers send the traffic to Router 4, who therefore receives the traffic twice.
Take a look at this diagram, and imagine that every router is in Dense Mode. Traffic goes from Sender to Router 1, at which point it’s sent out to both Router 2 and Router 3. Both these routers send the traffic to Router 4, who therefore receives the traffic twice.
We learnt earlier that if Router 4 doesn’t have an interested receiver, it will prune itself from the tree.
But hang on: if the router is operating in Dense Mode, then won’t it still forward the traffic it received from Router 3 onto Router 2? And won’t it forward the traffic it received from Router 2 onto Router 3? And won’t they both send it to Router 1, who’ll once again send each packet to the other router, and so on and so on until the end of time?
Luckily, there’s a way to stop this from happening, and it’s called an RPF check. RPF stands for Reverse Path Forwarding, and it’s used LOADS in multicast.
Here’s what our router checks when it receives traffic in a multicast stream: “when multicast traffic comes in on an interface, take the source IP address – the sender – and check the routing table* to see how you’d get to that source. Did the traffic come in on the interface you’d use if you wanted to go out to the source? If so, accept the traffic: it’s legit, and there’s no loops. But if it came in on any other interface, drop the traffic. You can’t guarantee that the traffic isn’t looping.”
*The phrase “check the routing table” is good enough for now, but in a moment you’ll see you can potentially check other places too.
When Router 2 receives the multicast packet from Router 1, it checks the source – 10.1.1.2 – and looks in its routing table to see which interface it would use to get to 10.1.1.2. In this case it would indeed use the interface out to Router 1, which means the RPF check succeeds. Therefore, Router 2 accepts the multicast stream from Router 1.
Later on, if Router 2 receives a packet from Router 4, Router 2 rejects it. The RPF check has failed. We prevented a loop!
Chances are though that Router 4 won’t forward anything on to Router 2 at all, because it’ll drop the stream it receives from Router 3. Look at that cost on the link between R3 and R4. The path from R1–>R2–>R4 is much better. Any multicast traffic R4 receives on its ge-0/0/1 interface will be sent directly to hell. DIRECTLY TO HELL!!
Where does it do these checks? By default Junos does it in inet.0, the default routing table. However, it is possible to also use a special table called inet.2, in situations where you might want to only use a select number of prefixes for RPF checks – or indeed, if you want to override them to actually point to somewhere else!
SOURCE-SPECIFIC MULTICAST: LINKING UP SENDERS AND RECEIVERS
In Dense Mode it’s easy for traffic to get from sender to receivers: the traffic is essentially flooded everywhere. It’s up to the routers to prune individual links off the tree if those links don’t have any interested receivers. By contrast, we mentioned that in Sparse Mode our routers have to actively join the tree.
 There’s actually two different methods that Sparse Mode can use to join up senders and interested receivers. Let’s focus first on the easiest of the two methods: the one where the IP address of the source is known in advance. Just to be clear, right now we’re talking about the receiver knowing the actual IP of the source, for example the address 10.1.1.2 in the diagram. Let me give you that diagram again, to save you scrolling back up.
There’s actually two different methods that Sparse Mode can use to join up senders and interested receivers. Let’s focus first on the easiest of the two methods: the one where the IP address of the source is known in advance. Just to be clear, right now we’re talking about the receiver knowing the actual IP of the source, for example the address 10.1.1.2 in the diagram. Let me give you that diagram again, to save you scrolling back up.
Imagine the last-hop router – Router 4 – receives an IGMP Membership Report from an interested receiver. If this Membership Report contains a specific source IP address that the host wants to hear multicast traffic from, the last-hop router simply sends a PIM Join message upstream, in the direction of the first-hop router that the source sits behind. As each router along the path forwards it on, the routers listen in, so they can be aware that they’re joining the tree.
When the PIM Join message finally arrives at the first-hop router, the tree is complete. Traffic is forwarded downstream, down the tree, from sender to receiver. Traffic only travels down the path that the PIM Join messages took.
There’s a name for this first method of linking up senders to receivers: it’s called Source-Specific Multicast, or SSM. As the name suggests, our receivers are requesting not just to receive multicast traffic from a particular group, but requesting also that the traffic come from a particular source.
Cool fact: only IGMP version 3 can indicate a specific source. Versions 1 and 2 can only request a group. Weirdly though, even though v3 has that big advantage, it tends to be v2 that’s more often deployed in real life.
HOW ARE PIM JOIN MESSAGES FORWARDED?
Hey: did you notice how I didn’t say “the last-hop router sends the PIM Join message to the first-hop router”, but instead I said that the last-hop router sends the Join “in the direction of” the first-hop router? I chose my words carefully there. (Which is a rarity for me. My idiot mouth says the wrong thing approximately seventy times a day. The worst one in recent memory was when I called a customer “Dad”. Luckily I managed to cough immediately after, and I don’t think she noticed.)
You might reasonably assume that these PIM Join messages are sent as unicast messages directly to the source. But interestingly, that’s not how it works. The PIM Join is crafted in such a way that the multicast source’s IP address is included not in the destination address of the IP header, but instead in the payload of the packet.
PIM Joins are actually sent to a destination address of 224.0.0.13. This is the All PIM Routers address, and they’re forwarded using RPF checks: the PIM Join is only sent out of the interface which you’d expect to receive traffic on from that source.
At this point you might be wondering: what’s the difference between doing a routing lookup for the multicast source, and doing an RPF check for the multicast source?
By default, they’re actually the same thing. There’s a direct correlation between the routing table and the RPF table. The routing table informs the RPF process of what interfaces traffic should come in on, and if we’re being precise, it’s an RPF check that decides how to forward the PIM Join, not a routing lookup.
The reason this distinction is important is because it’s possible to not use the routing table at all, and instead have your own separate table for RPF checks. This allows you to have an RPF table that is vastly different from the unicast routing table! We’ll learn about that in a future post. For now, just know that PIM Joins aren’t routed towards the source, but rather are sent away from the router on the interface that the RPF checks say source traffic should arrive on.
By the way: when we talk about a source and a multicast group, we write it as (S,G). It stands for “Source, Group”, but for some reason it’s actually pronounced “ess comma gee”. You know: because S is quicker than saying source, and G is quicker than saying group. Way, way quicker. Good job, inventors of multicast! Good job.
RENDEZ-VOUS POINTS
Now let’s talk about what happens when a receiver knows what group it wants to receive traffic on, but it doesn’t know the IP address of the source. Or perhaps the receiver doesn’t care where it comes from, as long as it’s destined to the group.
The host itself sends the request via IGMP as usual, and the request reaches its default gateway, the last-hop router. So far, so good. But… if there’s no particular source, then where does our router send the PIM Join message to? Hmm! Looks like we have what cowboys in the wild wild west used to call a “problem”.
The solution is to dedicate at least one router in the network to joining up senders and receivers. This router is called the “Rendezvous Point“, or RP. Rendezvous is of course French for “toasted baguette”. No wait, I made a mistake there. Forget I typed that, my delete button is broken. Rendezvous doesn’t mean that, it means meeting. The rendezvous point is where source and receiver meet, to become more than just friends, but lovers too. Actually, forget I said that as well.
ANY-SOURCE MULTICAST
If SSM is when we do source-specific multicast, ASM is when we do Any-Source Multicast. In ASM, we don’t mind where the traffic comes from. As long as it’s being sent to the group we’re interested in, it’s all good. We tell the rendezvous point that we’re interested, and then if the RP happens to know about a source that’s sending to that group, the RP forward the multicast traffic onto us.
There’s a special name for the tree that’s produced from this Sender-to-RP-to-Receiver tree: it’s called the Shared Tree.
You might be thinking at this point that our RP needs to have a strong amount of CPU and bandwidth to be the centre of all this traffic. But actually, no: this “shared tree” only exists for a very short amount of time. In fact, there’s two efficiencies that make this process much more scalable
First: the source only sends one of its multicast packets to the rendezvous point. This is actually sent as unicast, not multicast, because it’s a special kind of packet – it’s a PIM Register message. It’s sent directly from the FHR to the RP – from the first-hop router to the rendezvous point. This is enough to let the RP know that the source exists. At this point the RP can choose to join the tree in the usual way, if it knows about interested receivers. If not, the RP just keeps a record of the fact that the source exists, in case anyone wants to join in the future. In the mean time, the RP prunes itself from the tree, ready to re-join if necessary.
The second efficiency is like this: as soon as the multicast stream is forwarded on from the RP to a receiver, our receiver can look at the packet headers to discover the source. This means that the receiver can signal directly to the sender that it wants to receive the traffic.
Suddenly now we have a better and more efficient kind of tree: a source tree, otherwise known as a Shortest-Path Tree, or SPT, and it’s signalled in exactly the same way as source-specific multicast. Once this shortest-path tree is set up, the receiver can signal to the RP that it doesn’t need traffic from the shared tree any more. Our final-hop router prunes itself from the shared tree, and happily receives traffic only from the source tree. What a beautiful story! Thank you, rendezvous point! Thank you for being so kind and generous, rendezvous point! I love you, rendezvous point. I love you.
If (S,G) means (Source,Group), what do we call it during that time when we want a group, but we don’t know the source? We call it (*,G), said as “star comma gee”. Which is INFINITELY faster than saying “star comma group”. In fact, it’s so much quicker that I’m going to start calling pop groups “pop Gs”. Group psychology is now “G psychology”, and WhatsApp groups are now “WhatsApp Gs”.
THAT’S IT!
I mean, I say that’s it – of course, there’s so much more to multicast than this. More messages, more protocols, more customisation, more security, mo money, mo problems. But the theory in this initial should be enough for us to dive straight into configuration in our next post.
If you’re ready for more, click here to read Part 2, where we take a much closer look at IGMP. Mmmmm yes!
But wait! What’s that you say? You want to know how to find out when I make new posts? Well, lucky for you that I always post about them! If you’re on Mastodon, follow me to find out when I make new posts. (2024 edit: I’m also on BlueSky nowadays too. I was once on Twitter, but I’ve given up on it, on account of… well, I don’t need to finish that sentence, do I.)
And if you fancy some more learning, take a look through my other posts. I’ve got plenty of cool new networking knowledge for you on this website, especially covering Juniper tech and service provider goodness.
It’s all free for you, although I’ll never say no to a donation. This website is 100% a non-profit endeavour, in fact it costs me money to run. I don’t mind that one bit, but it would be cool if I could break even on the web hosting, and the licenses I buy to bring you this sweet sweet content.





I discovered your blog by chance and I love your casual and agile style, thank you very much. I am looking forward to your next post with the juicy multicast lab!!
Haha, thank you Mick! Oh boy is it juicy. 80% done with the next post, hopefully it’s coming very soon indeed!
Hi Chris,
I personally hate multicast as I have had so many issues with it – from killing CISCO 6900 switches (CPU straight to 100%) to issues with firewalls and much more.
But I must say this is the best introduction to multicast I have seen so far and I am looking forward to reading the following posts on this topic.
Keep up the great work
Shane
That’s incredibly kind of you to say so, thank you so much Shane! If you ever write any posts about the issues you’ve faced and how you overcame them, pass me the link and I’ll be sure to share it. 🙂
Chris,
Great post. Thank you very much. Your post has just helped me solidify me existing knowledge of Multicast. I found your article better explained compared to the Juniper coursework material.
Two things, that I found that might need correction: IGMP (Internet Group Management Protocol)
The other was:
Explanation on RPF check:
“When Router 2 receives the multicast packet from Router 1, it checks the source – 10.1.1.2 – and looks in its routing table to see which interface it would use to get to 10.10.10.10. ”
On this one I thought you meant to write, “which interface it would use to get to 10.1.1.2”.
As for RPF check, a route to the Multicast source address is checked.
Look forward to reading your remaining articles on Multicast.
Hi Birajan,
Gosh you’re right about that! Haha I must have been very tired to make that mistake on what IGMP stands for. I’ve corrected “Membership” to “Management”. Thank you!
And thank you for the RPF correction too. I’ve updated that, and given a brief mention of the Junos inet.2 table. I’ll expand on that in a future post.
Very grateful for those corrections!
Wont lie, i actually googled smoke RFC 69-420…
Regards,
Lish.