A COMPLETE BEGINNER’S GUIDE TO SUBNETTING

IP addresses were invented by William Shakespeare in the 16th century. He needed a way to remember each character in his latest play, “A Midsummer Night’s Dream About The Internet” – the play which itself famously spawned the very same World Wide Web that we all know and hate today. Who can forget such powerful characters as 192.168.10.5, 1.2.3.4 – and not forgetting the star of the show, 69.69.69.69.

Anyway, forget I said any of that. A very important part of networking is the concept of subnetting: the idea of taking a large block of IP addresses, and then dividing it up into smaller chunks that can be allocated to customers, or to certain parts of a network, like your corporate LAN, or a guest VLAN. If you’re corrupt you might even subnet off a few IPs for yourself to sell down the market, along with some bootleg DVDs, and those half-full bottles of gin you found in the bin that one time.

Subnetting can frequently confuse newcomers, and in my experience this is because the explanations don’t take the time to explain the philosophy of what you’re trying to achieve. Instead, they jump straight into some frankly baffling math. And to be clear, that math is important. But it’s no wonder that new students find it confusing when they don’t understand what they’re ultimately trying to achieve.

This post skips over all that math, in favour of philosophy. With that in mind, this post is written for folks who are brand new to subnetting, and even potentially brand new to networking. No prior knowledge is needed to understand this post: it is a guide to subnetting, for complete beginners.

This post will probably take you half an hour to read, and by the end of it you will feel like you have levelled up for sure. After reading this, you might even decide to go down the CCNA or JNCIA/JNCIS route, where you will come back and learn the math behind it all. Trust me: after reading that post, you’ll find that math way easier to understand.

Let’s do it!

 

FIRST, A PRIMER: WHY ARE IP ADDRESSES WRITTEN THE WAY THEY ARE?

The coolest celebrities can’t get enough of IP addresses. Beyonce wears one around her neck at all times. Calvin Harris regularly “spins” IP addresses on his “decks”. As for Bill Murray, legend has it that he collects rare IP addresses, hand-crafted in Milan and Paris, and keeps them in his private collection far, far underground, in the centre of the earth. Wow!

You’ve seen IP addresses before: they’re four numbers, separated by dots—and pretty much every computer on the internet has one. Here’s some examples of IP addresses:

8.8.8.8

10.0.15.30

192.168.100.230

(In particular, these are IPv4 addresses, as opposed to IPv6, which is very much a post for another day!)

You may already know that each of those four numbers can, in principle, be anything from 0 to 255. In other words, if you were to count all of the theoretical IP addresses, then the first one would be 0.0.0.0, then 0.0.0.1, then 0.0.0.2, all the way up to 0.0.0.255. Then you’d go to 0.0.1.0, then 0.0.1.1, and so on. Theoretically, 255.255.255.255 is the very last IP address.

This means that in total there are – theoretically – 4294967296 IP addresses. That’s almost 4.3 billion. Which coincidentally, is also the number of girlfriends I’ve had. Prove me wrong, nerds.

Fun fact: each of these numbers is called an octet. In other words, an IP address is made up of four octets.

255 might seem like an odd number for each octet to end at. There is a reason for that, which we’ll come on to shortly. For now, let’s talk about how each section of a bigger network will be assigned a block of IP addresses.

 

BLOCKS OF IP ADDRESSES

There’s a very high chance that your home network is powered by a router that your ISP gave you. That router was probably set up so that your home network uses a particular block of IPs, perhaps something like 192.168.1.x, where the x is anything from 0 to 255. In other words, your home network has been assigned a block of 256 IP addresses. (In reality you can’t use all 256 of them. There’s a few that are always reserved, and we’ll talk about how that works later on.)

In a way, you could say that this block of IPs – this IP range – is a sub-network of the bigger block of 4.3 billion IP addresses. And indeed, that’s exactly what subnetting is: taking a block of IPs, and then carving out a smaller block of IPs from it.

(Bonus fact: there is also a concept called supernetting, which does the opposite: it takes lots of smaller IP blocks, and combines them into one larger block!)

This idea of subnetting is a crucial part of designing a network.

For example, you might be given a big block of IPs, and then told that within that big block you need one subnet to host all your employee’s trusted computers, another subnet to host your phones, perhaps another for storage, and another for CCTV, yet another for guest Wi-Fi, and so on. Maybe you even have a VPN to a data center that hosts various applications. Your task is to choose IP ranges that are big enough to take all the machines in that part of the network, and allow for future growth – but without choosing an IP range that’s so big that you end up wasting IPs. You’ll also want to make sure that you choose ranges that don’t overlap with each other. That would be a disaster!

A key thing to understand is that you can’t just pick any random starting and ending IP. For example, you couldn’t have a LAN that had an IP range of 192.168.1.5 to 192.168.1.137. There are certain IPs that a block of IPs can start on. Then, depending on your starting IP, there are only certain IPs that the block can end on, depending on how big the block is.

Why is that? To understand that, we need to learn how computers talk to each other. It’s binary time!

 

WHAT IS BINARY?

You may know already that computers talk in “binary”. What does that mean?

When your computer is processing a calculation, or sending information to a disk, or sending information to a digital monitor or audio output, it’s doing so using a ridiculously fast series of electrical pulses. In fact, there’s two kinds of electrical pulse that it will use: a high pulse, and a low pulse.

Discs will do a similar thing, but instead of pulses, they’ll store magnetic charges that either point north, or south. The end result is the same though: conceptually, you can think of “high or low”, “north or south”, “on or off”.

For example, imagine a computer that very quickly sends eight electrical pulses that were something like low, low, high, low, low, low low, high. Perhaps instead of writing it like that, we could just use 0 to mean low, and 1 to mean high. That’s much easier to write out what the computer is doing: we could just say 00100001 instead of “low low high low etc etc”.

What does this combination of high and low pulses actually mean? That’s an interesting question, because it depends on what the computer has been programmed to do in the exact moment that it receives that series of pulses. For example, it could mean “make a specific pixel on a screen light up as orange”, or “move something in memory”, or “eject this disk” or “make a beep come out of a speaker”.

It could also represent text. There’s an old way of storing text called ASCII, where various combinations of eight 1s and 0s would represent different characters. In that system, “00100001” actually means lower-case “a”.

If you wanted to store an ASCII text file that simply said “hello”, the computer would store it on disc as a series of these 1s and 0s on a magnetic disc, such that we could write it like this: “01101000 01100101 01101100 01101100 01101111”. (No, I’m not a wizard that can talk computer binary as a second language: this handy website lets you put words in, to see how it would be represented in ASCII.)

Each 0 and 1 is called a bit, and when there’s eight bits in a row we call it a byte. 

 

LET’S LEARN TO COUNT IN BINARY!

In that example, “00100001” represents lower-case a, and the reason it represents that is because the computer will be programmed in that moment to interpret it as a text character.

However, in a different context, a computer receiving a series of high and low voltages written as “00100001” could represent a whole heap of other things, including just being a pure number. Check this out: below I’ve written 00100001 on the bottom row. Then on top of it, I’ve written a value for each bit in the 8-bit number. This is like when you were six, and you learned that the number 452 has a 4 in the hundreds column, a 5 in the tens column, and a 2 in the ones column. This time though, the columns have rather different values.

---------------------------------------------------------
VALUES: | 128 |  64 |  32 |  16 |  8  |  4  |  2  |  1  |
---------------------------------------------------------
BINARY: |  0  |  0  |  1  |  0  |  0  |  0  |  0  |  1  |
---------------------------------------------------------

Think of the numbers along the top as being like on/off switches. In this particular example, the values of 32 and 1 are both turned on. 32 + 1 = 33, so that means that 00100001 is the binary way of writing the number thirty-three.

You can actually make any number between 0 and 255 by “turning on” the various bits.

For example, if I wanted to make the number ten, I’d do this:

-------------------------------------------------
| 128 |  64 |  32 |  16 |  8  |  4  |  2  |  1  |
-------------------------------------------------
|  0  |  0  |  0  |  0  |  1  |  0  |  1  |  0  |
-------------------------------------------------

Eight plus two equals ten. Quick maths!

What if I wanted the number 160? That would be like this:

-------------------------------------------------
| 128 |  64 |  32 |  16 |  8  |  4  |  2  |  1  |
-------------------------------------------------
|  1  |  0  |  1  |  0  |  0  |  0  |  0  |  0  |
-------------------------------------------------

128 + 32 = 160.

And what about the number 255? That’s like this, with all of the binary “switches” turned on:

-------------------------------------------------
| 128 |  64 |  32 |  16 |  8  |  4  |  2  |  1  |
-------------------------------------------------
|  1  |  1  |  1  |  1  |  1  |  1  |  1  |  1  |
-------------------------------------------------

128 + 64 + 32 + 16 + 8 + 4 + 2 + 1 = 255!

That, right there, is the reason that octets in an IP address can only go up to 255. It might seem like a totally arbitrary number, but there is actually a reason for it!

We’ll come back to binary in a moment. For now, let’s have a quick history lesson.

 

CLASSFUL ADDRESSES

The internet, and IP addresses, were both invented in a time when no-one could possibly imagine what the internet would later become. You have to remember that this is a time when the idea of “web sites” was the stuff of pure science fiction. If you’d have told someone in the year 1980 that they could one day use their experimental internet, their academic networking project, to watch high-resolution videos of teenagers licking toilet seats on planes to prove that coronavirus isn’t real, they’d simply look at you confused and astonished.

With that in mind, the way that IPs were originally allocated may seem very wasteful by today’s standards, but probably made sense at the time. RFC 791, written in 1981, defines three “classes” of IP address. In this old system, the class that an IP address is in told you how many IP addresses are in that block of IPs.

“Class A” addresses are any IPs that begin with an octet from 0 to 127. To be clear, example IP addresses include 1.2.3.4, 72.56.231.99, and 127.128.129.210.

If an IP address is in the Class A range, then it belongs to a block where the owner gets over 16 million IP addresses all to themselves – because the first octet defines the entire block!

So for example, 48.x.x.x – that is to say, 48.anything.anything.anything – was given to the Prudential Insurance Company of America, who still own that entire block to this day. 17.anything was given to Apple, and 19.anything was given to the Ford Motor company.

Let’s do a “whois” on the IP 48.1.2.3 and see what it says:

chrisparker@Chriss-MacBook-ARM ~ % whois 48.1.2.3
{many lines omitted}

organisation:   Prudential Securities Inc.
NetRange:       48.0.0.0 - 48.255.255.255
CIDR:           48.0.0.0/8
Organization:   The Prudential Insurance Company of America (PICA-3-Z)

That confirms it: Prudential own the entire block, from 48.0.0.0 all the way up to 48.255.255.255. Blimey. That’s a lot of IP addresses!

Moving on, next is the “Class B” range.

A Class B range used the first two octets to indicate how many IP addresses you got. Any IP starting with 128, all the way up to any IP starting with 191, was part of the Class B range. So for example, one organisation might have been given 128.5.x.x, while another might have been given 142.219.x.x. In total that’s 65,536 theoretical IPs that they get all to themselves.

You may already spot a problem here. An organisation can get 65,536 IPs, or over 16 million IPs… but nothing in between. And with that in mind, check this out: the final one was Class C addresses, which was any IP starting with 192, all the way up to 223.

In a Class C block, the first three octets defined how big your network was. So for example, 194.129.5.x, 210.123.111.x, and 223.9.8.x are all examples of Class C blocks. This gave you 256 address in total, because you could have (for example) 223.9.8.0 all the way up to 223.9.8.255.

 

CLASSFUL ADDRESSES WERE A TERRIBLE IDEA

You may now be thinking to yourself, “Wow, that’s wasteful. So I can either have 16 million addresses, or 65536 addresses, or 256 addresses – and nothing in between?” And indeed, in the olden days, that was absolutely correct! In fact, the reason that some very large orgs have such massive blocks of IP addresses today is because of this old classful system.

This was particularly a problem considering that we were, and still are, very much running out of IP addresses. In fact, depending on your perspective, we already have run out of addresses. This Wikpedia article actually says that Stanford University used to own the 36.x.x.x Class A block, but they gave it back to aid in delaying IP address exhaustion.

It gets worse. “Class D” was reserved for multicast. This IP block is 224.x.x.x all the way up to 239.x.x.x. That’s a whopping 268 million IP addresses. And let me ask you: how often is multicast actually used? Not enough to have so many IP addresses given to it.

It gets even worse still. “Class E” is, to quote RFC 988, “reserved for future addressing modes”. This is 240.x.x.x all the way up to 255.x.x.x. Well guess what: we’re in the future now, and we’re running out of IP addresses. But here’s the twist: we can’t actually use this Class E block.

Why? Because even if we did decide to start using them, we have the problem of there being hundreds of millions of machines in the world that have been programmed to know that this block of IP addresses is not yet valid to be used! Imagine being given a block of IPs that half your customers can’t get to. Hardly ideal.

(Interesting fact: I have heard tale that some very, very large orgs – large enough to program their own network stack on their devices – are actually using the Class E range internally, basically using it as a new, massive private IP range. Nice!)

So, when we say there’s 4.3 billion theoretical addresses… the real number is far smaller than that.

Even just focusing on Classes A, B, and C, it’s clearly wasteful. If an org just wanted eight IP address, there was no choice but to give them 256 addresses. If an ISP wanted something like a few thousand IPs, they’d have to either be given individual blocks of 256 addresses, or a massive block of 65,536. Classful addressing didn’t scale, and IPs were running out really, REALLY fast.

So, the networking world essentially scrapped the idea of classful addresses altogether. People who “owned” particular blocks often got to keep those blocks (cough Ford cough Prudential cough), but they were no longer referred to as classful addresses.

Instead, a new way of subnetting called “classless” addressing came in.

 

CLASSLESS INTER-DOMAIN ROUTING

The idea behind classless addressing is that classes in the old sense no longer exist. In the year 2021, we don’t care in the slightest about class A or B or C, apart from to understand historical context, and to go “wow, that random company sure does have a lot of addresses”.

Instead, classless addressing allows us a lot more flexibility in the number of IPs you can have in a network. Let’s take a look again at the values in each column of that binary counting system.

-------------------------------------------------
| 128 |  64 |  32 |  16 |  8  |  4  |  2  |  1  |
-------------------------------------------------

See each of those numbers? Thanks to classless addressing, you can now have a block of IPs which contains any of those numbers. You could have a block with 8 IPs, 16 IPs, 32 IPs, 128 IPs, 256 IPs… and indeed, you can keep going. Notice that as you go to the left, the number doubles. 1, 2, 4, 8, 16, 32 – it doubles each time. So you can imagine that after 256 you get 512, then 1024, then 2048, then 4096, and so on. As such, you can have a block that contains 512 IPs, 1024 IPs, and so on.

The formal name for this system is “Classless Inter-Domain Routing”, or CIDR for short, which is exactly the name of RFC 1519 that defines it. In casual conversation engineers will just talk about subnetting, but you’ll definitely see the term CIDR a lot around the place. In fact, if you scroll up and look at that WHOIS again, you’ll see it on the output.

To achieve this, CIDR introduces the concept of a “subnet mask”, which is a number that tells us how many IPs are in a block. With a little bit of binary counting, we can also take any IP address, look at its subnet mask, and work out exactly what the first and last IP address is for any subnet mask.

To understand how subnet masks work, I’m first going to tell you an easy-to-understand version which doesn’t tell the full story. Then, once you get that, we’ll build on that knowledge. Stick with me!

 

SUBNET MASKS – THE EASY EXPLANATION

Sometimes you’ll configure your network settings manually. More often, you’ll get them automatically via DHCP. DHCP itself is a post for another day, but basically the D stands for Dynamic: your computer calls out for network information, and your router (or a dedicated DHCP server) will automatically reply with three essential pieces of information:

• Your IP address
• Your subnet mask
• Your default gateway

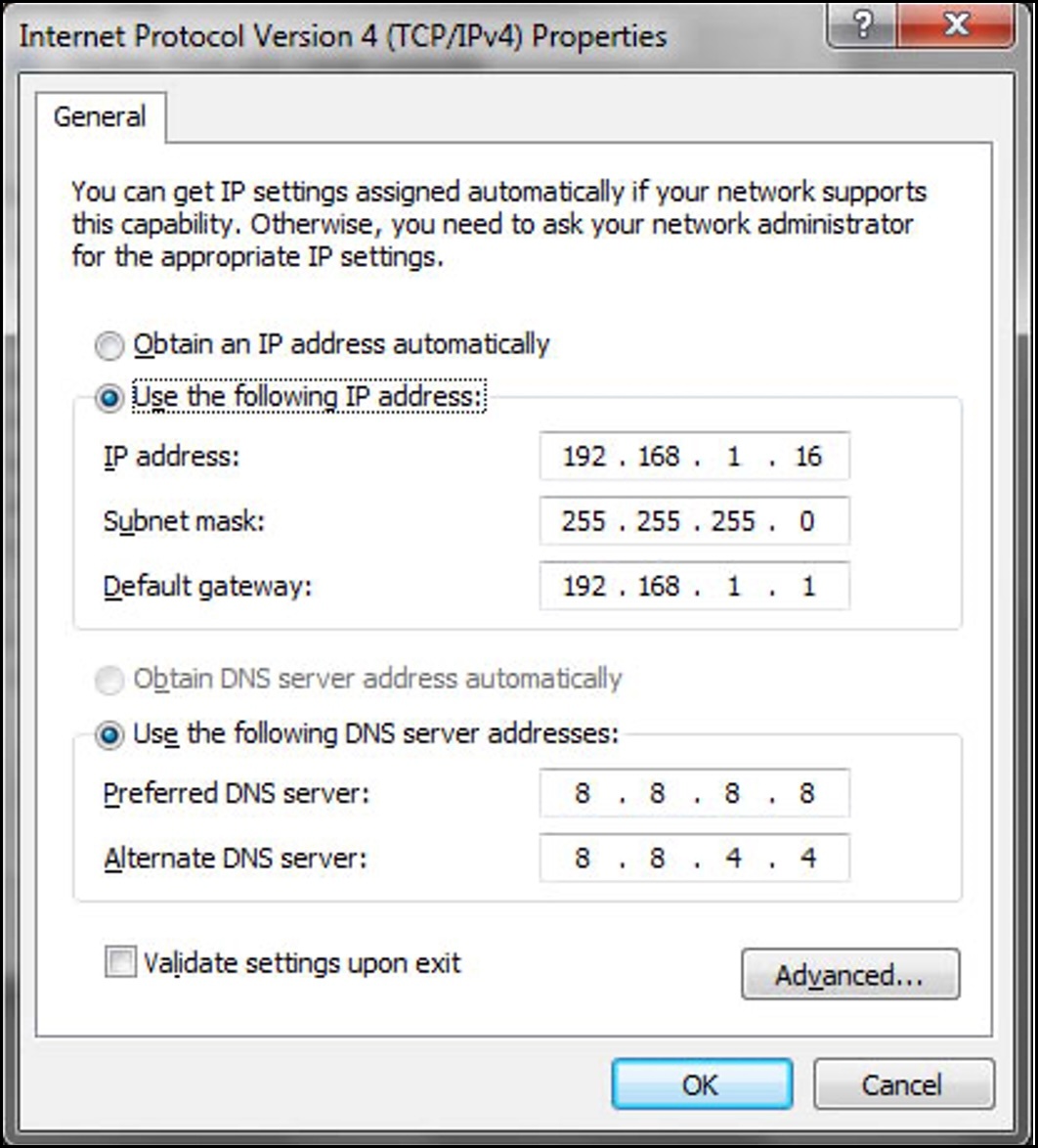
Let’s talk about those first two pieces, by looking at this screenshot of the IPv4 settings on a Windows network card.

This person has typed them in manually. Notice that their IP address is 192.168.1.16, and their subnet mask is 255.255.255.0. Notice too that the subnet mask is written in a similar way to an IP address: four numbers, each with a dot in between.

Let’s write these numbers on top of each other.

Here’s the concept. When a number in the subnet mask is a 255, the equivalent number above it in the IP address cannot change. However, when the number in a subnet mask is a zero, the equivalent number in the IP address can indeed change.

That means that in this example, the first three octets of the IP address – 192.168.1 – cannot change, but the final number can be anything from 0 to 255. That means that our block of IPs here is 192.168.1.anything, giving us a block of 256 IP addresses in total, from 192.168.1.0 up to 192.168.1.255, and anything in between.

A subnet mask kind of “locks in” a section at the start of the address, and then lets you do what you like with the rest. In fact, for that very reason, we often call that first section (192.168.1 in this case) the “network” part of the address, and the rest of it the “host” portion, because that’s the bit that you’re free to assign to your hosts.

If you had a subnet mask of 255.255.0.0, this would mean that the first two octets were the “network” portion, and you could do anything you like with the other two host octets. That subnet mask gives you 65,536 IPs to play with.

 

SLASH NOTATION

Before we take subnet masks to the next level, here’s something cool.

If you were to write out 255.255.255.0 in binary, it would look like this:

   255  .   255  .   255  .   0
11111111.11111111.11111111.00000000

There are twenty-four 1s in a row there. As such, a much cleaner and quicker way of writing 255.255.255.0 is to simply write it in “slash notation”, which looks like this:

/24

Wow. That’s much easier to write! And yet, amazingly, a lot of computer and network OSs don’t let you write it like this. Instead, they insist that you give up valuable seconds of your time to write it out in the long-form of 255.255.255.0.

As for 255.255.0.0, you could alternatively write that simply as /16. Slash notation is real nice!

 

SUBNET MASKS – THE NEXT LEVEL

Up until now, our example subnet masks just give us the same amount of IPs as the classful addressing scheme, in that our example subnets have either given us 256 IPs, or 65,536 IPs.

However, the explanation of the binary of it all actually hints at how subnetting allows us to do far more than that.

Let’s imagine that we wanted a subnet that contained 128 addresses. To do that, we would use a subnet mask of 255.255.255.128. Why is that? Well, let’s take a look at what that number looks like if we write it in binary:

   255  .   255  .   255  .   128
11111111.11111111.11111111.10000000

Did you notice how, in the final octet, there is now a 1 at the start? I’ve highlighted it in red above. Well, with that in mind, let’s now give a more accurate definition of how subnet masks work.

Earlier on we said that if an octet in the subnet mask was 255, then the equivalent number in the IP has to stay the same. That is true, but there’s a bit more to it than that – because it would be more accurate to say that this actually happens on a bit-by-bit level, like this:

192 . 168 .  1  . 16 :     11000000.10101000.00000001.00010000
255 . 255 . 255 . 0  :     11111111.11111111.11111111.00000000

In other words, if a bit in the subnet mask is set to 1, then the equivalent bit in the IP address also has to stay the same. But if the bit in the subnet mask is a zero, then you can do whatever you want with it!

And with that in mind, I bet that a subnet mask of 255.255.255.128 suddenly becomes a whole lot easier to understand. Imagine if I told you that we had a block of IPs that started at 192.168.1.128, and we have a subnet mask of 255.255.255.128. Let’s draw this out in binary:

192 . 168 .  1  . 128:     11000000.10101000.00000001.10000000
255 . 255 . 255 . 128:     11111111.11111111.11111111.10000000

That final 1 in the last octet means that the bit above it can’t change. But as for the other seven bits, you can do what you like! That means that the final octet in the IP address can be anything starting from 128 (10000000) up to 255 (11111111).

Here’s some examples:

• 192.168.1.129 (10000001)
• 192.168.1.130 (10000010)
• 192.168.1.200 (11001000)
• 192.168.1.254 (11111110)

Here’s a quick exercise for you:

• Try writing out the subnet mask 255.255.255.192 in binary.
• Now try writing out the IP address 192.168.1.64 in binary.
• Finally, if I told you that 192.168.1.64 was the first address in a block of IPs, and 255.255.255.192 was the subnet mask, can you see if you can work out what the final IP in the block is – and how many IPs there are in total? If not, click this link to see the answer: it’s a link to a subnet mask calculator, with this exact question already answered.
• Bonus points if you can work out the slash notation for that subnet mask!

 

SOME OTHER EXAMPLES OF SUBNET MASKS

So in total, subnet masks go from /32 (255.255.255.255, which means a single host machine) to /0 (0.0.0.0 – the entire internet).

If you want a full list of every subnet mask, give this excellent cheat sheet a look, by Jeremy at PacketLife. I’ve regularly printed this out and given it to new 1st liners in orgs that I’ve worked for.

(UPDATE, NOV 2024: Since writing this post, I’m sad to say that PacketLife seems to be permanently offline. For this reason alone, I’ve uploaded a copy of the subnetting cheat sheet. I did not make this PDF. All credit goes to Jeremy Stretch. I that the author won’t mind me serving this file on my own domain. Once you’ve progressed a little in your networking studies, please follow him on GitHub, and check out his NetBox project for administering network automation.)

In any case, it’s well worth memorising the subnet mask, slash notation, and IP size of the /32, /30, /29, /24 and /23 ranges, because you’ll see them the most.

• /32 (255.255.255.255) is the subnet mask for a single machine, because every single bit in the subnet mask is set to 1. In other words, nothing can change. You would use this on the loopback interface of a router, or in a firewall rule that refers to a specific machine.
• /29 (255.255.255.248) gives you eight IPs. If you buy a corporate internet connection from an ISP, it’s common for you to get a block of eight public IPs with it.
• /24 (255.255.255.0) is very common on a LAN. It gives you 256 IPs. If you need more, you can jump up to /23, which is written as 255.255.254.0. This gives you 512 IPs. That might seem like a big jump, but in practice this is almost always done using private IP addresses, so it’s generally not as wasteful as it might seem.
• As for /30 and /31, we’ll come back to those in a moment.

One final thing. Do you remember that we mentioned how the first section of the address is called the “network” portion? For this reason, network engineers also often use the word “prefixes” to refer to routes that a router learns or advertises. The word comes from the fact that we’re learning blocks of IPs rather than each individual IP address, and so the router only really cares about the first portion of the address, or the “prefix”, along with the subnet mask. That is as opposed to the host portion, which you could call the “suffix”.

 

THE FIRST AND LAST IP IN ANY RAGE IS RESERVED

Up until this point we’ve said that 255.255.255.0, or /24, gives you 256 IP addresses. This is true. But to be more precise, you only get 254 usable addresses.

This is because the first and last IPs of any block of IPs are actually reserved. Check it out:

• The last IP in any block is known as the “broadcast address”. If you send traffic to this address, it gets sent to everyone on the subnet. You personally would rarely do this, but your computer does it all the time to work out what other machines are on the network.
• The first IP in any block is known as the “network address”. Technically this address doesn’t have an actual “use”. Rather, it just defines where the block of IPs begins. For reasons unknown to me, it was decided that this was enough reason to “reserve” this IP so that it can’t actually be used.

If you’ve got a LAN of 192.168.1.0/24, the last IP in your range – the broadcast address – can never be used by a host. That would be 192.168.1.255 in this case.

The first IP – the network address – also can’t be used on a LAN. In this case, that would be 192.168.1.0.

Here’s something to consider though. Imagine that we had a LAN with a /23 subnet – that’s 255.255.254.0, which gives us 512 addresses. Let’s imagine that we have the address range 192.168.2.0/23 for our LAN. That gives us a block of 512 IP addresses, from 192.168.2.0 up to 192.168.3.255. Check it out:

192 . 168 .  2  . 0  :     11000000.10101000.00000010.00000000
255 . 255 . 254 . 0  :     11111111.11111111.11111110.00000000

Do you see how the third octet in the subnet mask is 254? Notice how, when it’s written in binary, the final binary digit is a 0. That means that the bit above it in the IP is allowed to change. At the moment it’s written as 00000010. Well, if we can only change the final bit, then that basically gives us two options:

Decimal 2, aka binary 00000010
Decimal 3, aka binary 00000011

That’s why this subnet masks gives us IPs of 192.168.2.anything, and also 192.168.3.anything. That’s 512 address in total. That’s a really important aspect of classless routing: you’re no longer bound to “just” 256 addresses. Instead, you can actually have subnets that contain even more IPs than that! The boundary is no longer at the octet itself, but instead is on a bit-by-bit level.

With that in mind, here’s a question. In this network, can I assign the address 192.168.2.255 to a machine? The answer…. is yes! Remember that this subnet mask gives us a block of 512 IPs, not two blocks of 256. That means that apart from the first and last address (192.168.2.0 and 192.168.3.255) we can use any IPs we like, including 192.168.2.255, and 192.168.3.0. Nice!

 

ACTUALLY… SOMETIMES, YOU CAN USE THE FIRST AND LAST ADDRESS!

Interestingly, some computers and devices will actually let you use the network address – the first address in a range. But other devices won’t, and you’ll get problems communicating between them on the network, so you’re better off just not using it even if you can.

However, imagine that you had a block of eight public IPs, something like 203.0.113.8/29. That would give you 203.0.113.8 up to 203.0.113.15. It is quite common for an organisation to configure this range on a firewall, in such a way that it doesn’t belong on a particular interface, but instead belongs to a pool of IPs that can be NATted – that is to say, translated into a private address.

For example, you might configure the firewall to say “if you receive any traffic destined to 203.0.113.9, translate the address to 192.168.1.5”.

In this situation, interestingly, you often actually can use the network and broadcast addresses, because these addresses aren’t assigned to a LAN in the traditional sense. There is no “broadcast” in this situation, because the block of eight IPs isn’t tied to an actual interface: each IP almost acts on its own from the perspective of the NAT rules. Depending on your firewall vendor, you might legitimately be able to use all eight IPs!

I only mention that because some books will say that you can never ever use the first or last IP in a range. In actual fact though, that isn’t strictly true.

In fact, with that in mind, there’s one other situation where you can use the first and last address.

 

/31 – A SUBNET MASK WITH JUST TWO IPs

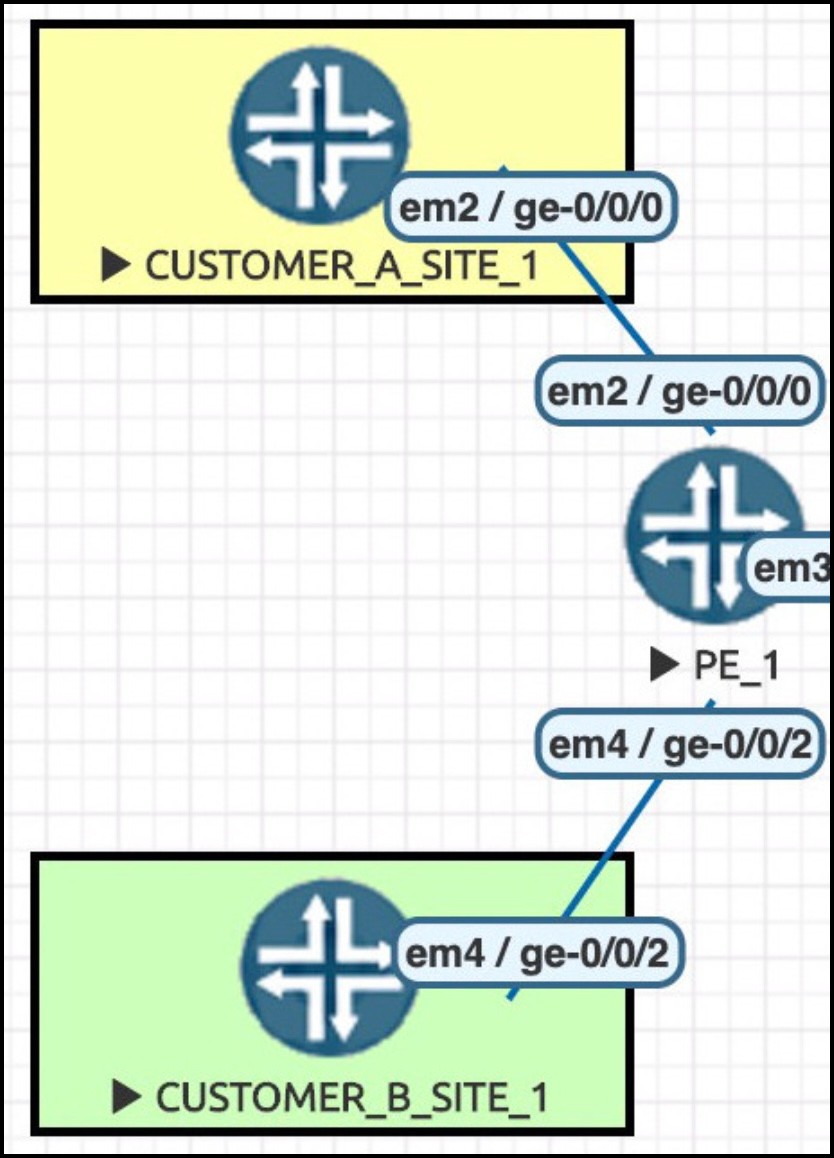Here’s an interesting one: think of a point-to-point link. This picture shows three routers. The top router has cable running straight to the middle router. Then, the middle router has a link straight to the bottom router. Each of these links are their own subnet; there are no other machines on that part of the network.

So: two routers, connected directly together. You need to give them each an IP, and you need to choose an appropriate subnet mask that doesn’t waste IP addresses.

You only really need two IPs for the subnet, right? One for Router A, and one for Router B. So perhaps a /31 – that is, 255.255.255.254 – might be appropriate. After all, if you check your subnet mask cheat sheet, you’ll see that this would give you two IPs exactly, right?

But here’s the catch. Remember that the first and last IP of any block is reserved. You can’t use them. That means that both IPs in the range have already been used before you’ve even had a chance to allocate them!!

Up until about a decade ago, it was exactly this reason that led many organisations to actually use a /30 – that is, 255.255.255.252 – for point-to-point links. This gives you four IPs, of which two are reserved, leaving you with two usable.

Hmm. Well, that does the job – but it’s pretty wasteful, right? Scale that out to a service provider network of many hundreds of links, and you’ll burn through IPs pretty quickly.

That’s why, in December 2000, RFC 3021 changed things. This RFC is called “Using 31-Bit Prefixes on IPv4 Point-to-Point Links”, and it makes an exception to the /31 subnet mask.

After all, what sense does it make to have a “broadcast” address on a subnet with only two IPs, where the two devices are plugged into each other directly? No sense! No sense, is what it makes. And as for the network address (the first address in the range), we’ve said before that it isn’t really “used” on the link, it’s more informational. So, this RFC liberates the /31 subnet mask so that it can indeed be used on point-to-point links.

RFCs take a while for vendors to adopt, and for the community to realise it’s a possibility. Even when more progressive vendors adopt it quickly, others may be slower, leading to inter-operational issues. As such, it took a little while to really take hold. But in the year 2021, any decent networking device will allow this subnet mask on an interface, and you’ll very commonly see it on core links.

 

ONE THING TO NOTE WHEN LOOKING AT ROUTING TABLES

Apart from understanding the history of networking, and understanding why certain IP blocks have been allocated in the way they have been, there is one other reason to understand classful ranges: for reasons that absolutely baffle me, when you look at a routing table on a router, some vendors to this day present this information to you by showing you a classful range, and then showing you the individual classless addresses underneath it.

So for example, if you’ve got four LANs in your network, and you’ve assigned them 10.10.10.0/24, 10.10.20.0/24, 10.10.30.0/24, and 10.10.128.0/23, the router OS might say “10.0.0.0/8 has been variably subnetted 4 times”, and will then list those four subnets underneath it.

Personally, I think that’s absolutely bonkers in the year 2021. Classful addressing is long dead, and I couldn’t care less that 10.0.0.0/8 has been subnetted! What I care about is the four CIDR prefixes. You know: on account of it being the year 2021.

In any case, earlier when I said that we don’t care in the slightest about classful addressing, it would in fact be more accurate to say that we don’t care, unless we’re using a networking OS that still insists on displaying routes by referring to the classful address. Lol.

Y’all know I’m a Juniper guy. If you do a “show route” on Junos, it just lists all the prefixes in numerical order, along with their slash-notation subnet mask. Real easy to read!

 

A FINAL NOTE ON TERMINOLOGY

Although this post is long, I want to end on something that makes me cross when I hear it, and which I can help you to avoid.

There are some situations nowadays when someone might describe themselves as having a Class A/B/C subnet – and almost all of these situations should make you raise an eyebrow.

Perhaps you’re talking with the head network architect at Apple or Ford or Prudential, who says they have a Class A block. They’re technically correct. That one is fine.

Perhaps you’re talking with someone who has decided to use 192.168.10.0/24 for their LAN, and describes this as using a “Class C block”, or a “Class C subnet mask”. This situation is interesting. They’re technically not wrong, but remember that classful addressing doesn’t exist any more. As such, many network engineers just think that using a term like this is a bit weird in the year 2021. It’s much more correct and useful to say “I’m using 192 dot 168 dot 10 dot 0 slash 24”, or even just “192 dot 168 dot 10 slash 24”, because the final zero is implied from the subnet mask. If you describe your network in terms of the classful addresses it uses… well, you can see why it’s a bit archaic.

But here’s the one that really makes me cross. Perhaps you’re talking with someone who says “I’m using 10.20.30.0 on my LAN with a Class C subnet mask”.

NO NO NO NO NO NO NO NO. NO YOU’RE NOT. NO. NO!!

You can see what they’re trying to say: a Class C range had 256 addresses, and a /24 (255.255.255.0) also has 256 addresses. But firstly, the IP they’re using isn’t in the Class C range, and secondly, it’s confusing as hell to describe it like that. Pure nonsense. If you hear someone describe things like that, don’t let them get away with it! It’s the enemy of clarity – and again, completely unnecessary in the modern world.

 

THAT’S IT!

Or at least, that’s it for this blog post. Now that you can read subnet masks and know how many IPs are in a block, in both CIDR style or slash notation style, you’re well on your way to being able to sit down and work out by hand some of the trickier problems of subnetting!

For example: if someone gave you 192.168.128.0/20, and said “I need one LAN that can host 300 machines, another that can host 65 machines, and another that can host eleven machines”, see if you can work out the most efficient way to do it. It’s okay to have unused IPs in each block, and it’s okay to also not use the entire /20 range. That’s a real advanced one, so don’t worry if you’re not sure how to do it. When you study a vendor cert, you’ll go over the math of subnetting over and over again, and it will soon become second nature to you.

Before I leave you, here’s a protip. In exams, make sure to be aware of when you’re being asked “how many IPs are in this subnet” versus “how many usable IPs are in this subnet”. The two questions are subtly different! If the exam has been written correctly, each of these two questions has a different answer.

If you enjoyed this post then I’d love it if you shared it on your favourite social media of choice.

If you’re on Mastodon, follow me to find out when I make new posts. (2024 edit: I’m also on BlueSky nowadays too. I was once on Twitter, but I’ve given up on it, on account of… well, I don’t need to finish that sentence, do I.)

And if you fancy some more learning, take a look through my other posts. I’ve got plenty of cool new networking knowledge for you on this website, especially covering Juniper tech and service provider goodness.

It’s all free for you, although I’ll never say no to a donation. This website is 100% a non-profit endeavour, in fact it costs me money to run. I don’t mind that one bit, but it would be cool if I could break even on the web hosting, and the licenses I buy to bring you this sweet sweet content.

Thank you very much for reading!